X

Fortrolighed & Cookies

Dette websted bruger cookies. Ved at fortsætte accepterer du brugen af dem. Få mere at vide, herunder hvordan du styrer cookies.

Godt!

Reklamer

En spiral er en kurve, der “udgår fra et punkt og bevæger sig længere væk, efterhånden som den drejer rundt om punktet”.

Der findes mange forskellige typer af spiraler, afhængigt af de formler, der skaber dem. I dette blogindlæg vil jeg diskutere todimensionelle spiraler (bemærk, at der også findes en række tredimensionelle spiraler).

Arkimedisk spiral

Dette er en spiral opkaldt efter den berømte græske matematiker Archimedes, som var den første til at beskrive den i sin bog Om spiraler. Den beskrives ved følgende polære ligning:

\, r=a+b\theta

hvor a og b er reelle tal.

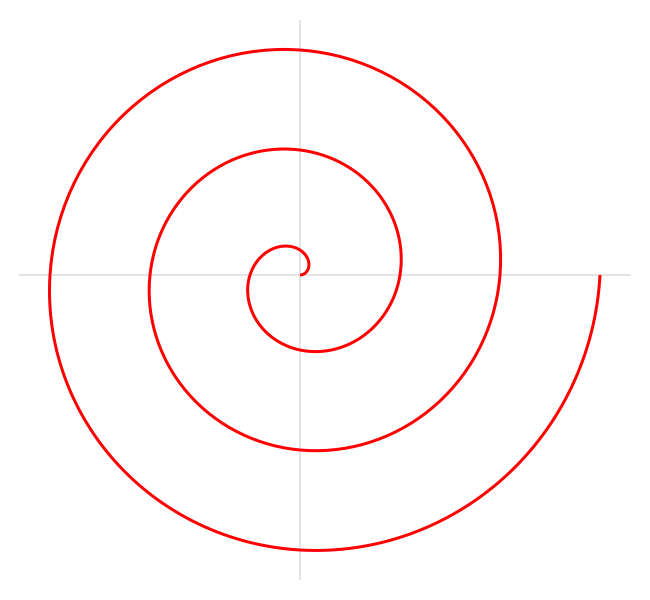
Gennem at ændre parameter a vil spiralen dreje, og parameter b styrer afstanden mellem de på hinanden følgende drejninger.

Fermats spiral

Fermats spiral er en parabolisk spiral, der adlyder følgende polære ligning:

r=\pm \theta ^{1/2}\,

Det er en type af Archimedisk spiral.

Euler-spiral

Også kendt som en Cornu-spiral, er det en kurve, hvis krumning vokser, når afstanden fra oprindelsen øges; “krumningen af en cirkelkurve er lig med den reciprokke af radius”.

Parameterformen består af to ligninger med Fresnel-intervaller, som kun kan løses tilnærmelsesvis.

S(x)=\int_0^x \sin(t^2)\,\mathrm{d}t,\kvad C(x)=\int_0^x \cos(t^2)\,\mathrm{d}t.

Disse integraler, og dermed Eulers spiral, kan bruges til at beskrive energifordelingen af Fresnels diffraktion ved en enkelt spalte i bølgeteori.

Hyperbolisk spiral

Den hyperboliske spiral, der først blev udtænkt af Pierre Varignon i 1704, er en transcendental kurve, hvilket betyder, at “det er en analytisk funktion, der ikke opfylder en polynomiel ligning”. Den er det modsatte af en arkimedisk spiral og har således følgende polære ligning:

r={\frac {a}{\theta }}

I centrum ligger den i uendelig afstand fra polen; for θ, der starter ved 0, starter r ved uendelig.

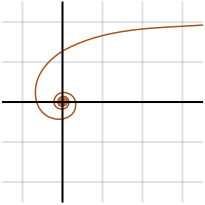
Lituus

Lituus er en spiral med en polær ligning:

r^2\theta = k \,

hvor k er en konstant. Vinklen er således omvendt proportional med kvadratet på radius.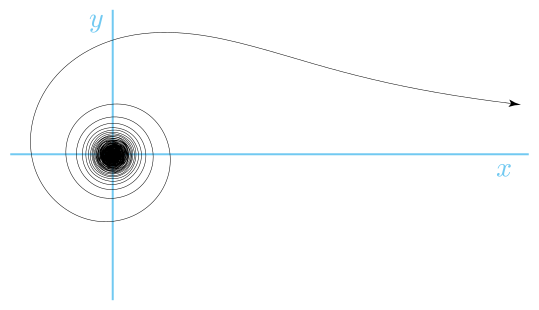

Kurven blev opkaldt efter den gamle romerske lituus (en buet augurstav eller krigstrompet) af Roger Cotes i en samling af artikler offentliggjort i 1722.

Logaritmisk spiral

Den logaritmiske spiral er en selvlignende spiral, som ofte optræder i naturen. Den blev først beskrevet af Descartes, men blev studeret indgående af Jacob Bernoulli, som kaldte den “den vidunderlige spiral”. Den har en polær ligning på