Implementering af dybdeførste søgning for det binære træ uden stak og rekursion.
Binary Tree Array
Dette er et binært træ.
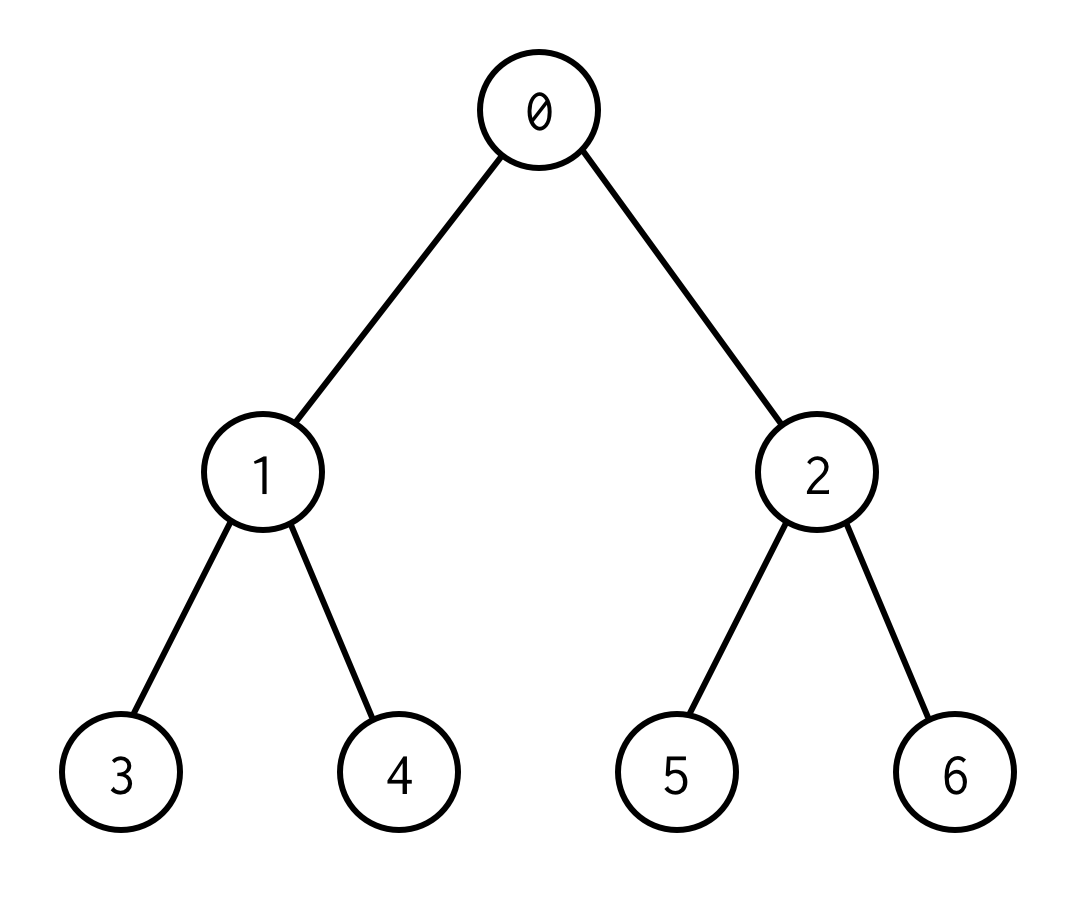
0 er en rodknude.0 har to børn: venstre 1 og højre: 2.
Hver af dens børn har deres børn og så videre.
Noderne uden børn er bladknuder (3,4,5,6).
Tallet af kanter mellem rod- og bladknuder definerer træets højde.
Træet ovenfor har højden 2.
Standardmetoden til at implementere binært træ er at definere en klasse kaldet BinaryNode
public class BinaryNode<T> { public T data; public BinaryNode<T> left; public BinaryNode<T> right;}Der er dog et trick til at implementere binært træ ved kun at bruge statiske arrays.Hvis du opregner alle knuder i binært træ efter niveauer startende fra nul, kan du pakke det ind i array.
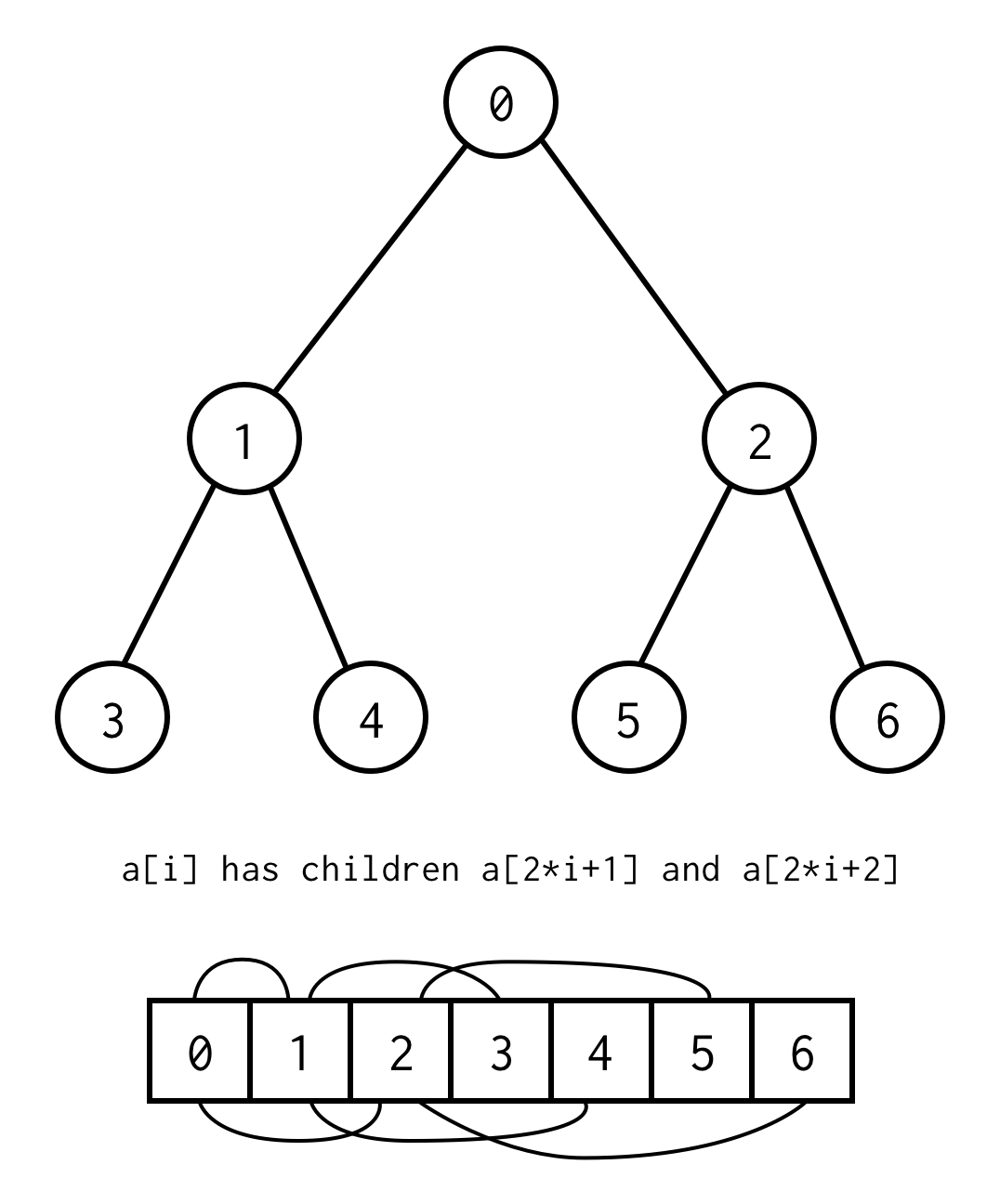
Forholdet mellem forældreindeks og børneindeks,giver os mulighed for at flytte fra forælder til barn, såvel som fra barn til forælder
left_child(i) = 2 * i + 1right_child(i) = 2 * i + 2parent(i) = (i - 1) / 2Vigtig bemærkning, at træet skal være komplet, hvilket betyder, at det for den specifikke højde skal indeholde præcis elementer.
Du kan undgå et sådant krav ved at placere null i stedet for manglende elementer.Opregningen gælder stadig også for tomme knuder. Dette skulle dække ethvert muligt binært træ.
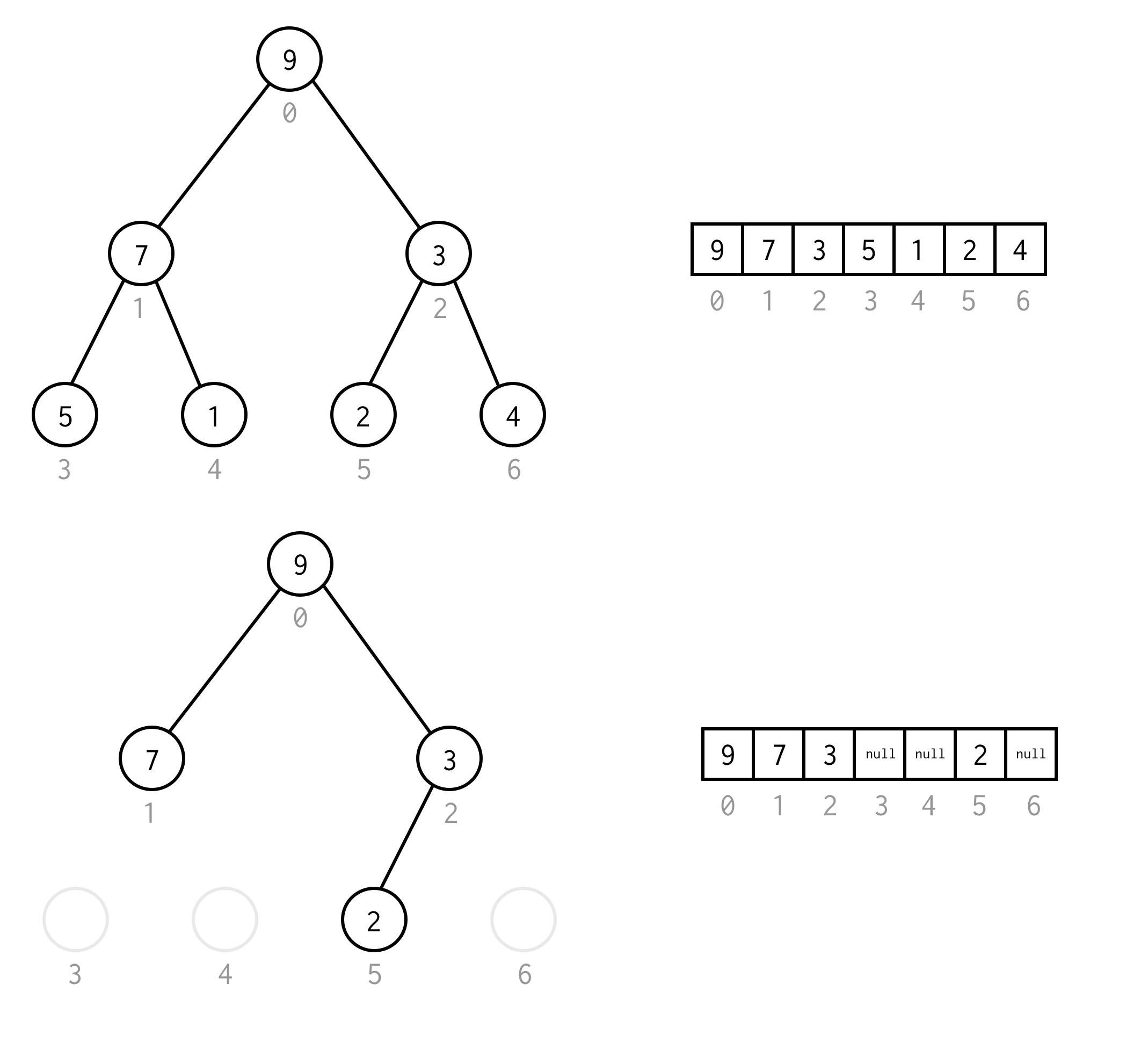
Sådan array-repræsentation for binært træ vil vi kalde Binary Tree Array.Vi antager altid, at det vil indeholde elementer.
BFS vs DFS
Der findes to søgealgoritmer for binære træer: BFS (breadth-first search) og DFS (depth-first search).
Den bedste måde at forstå dem på er visuelt
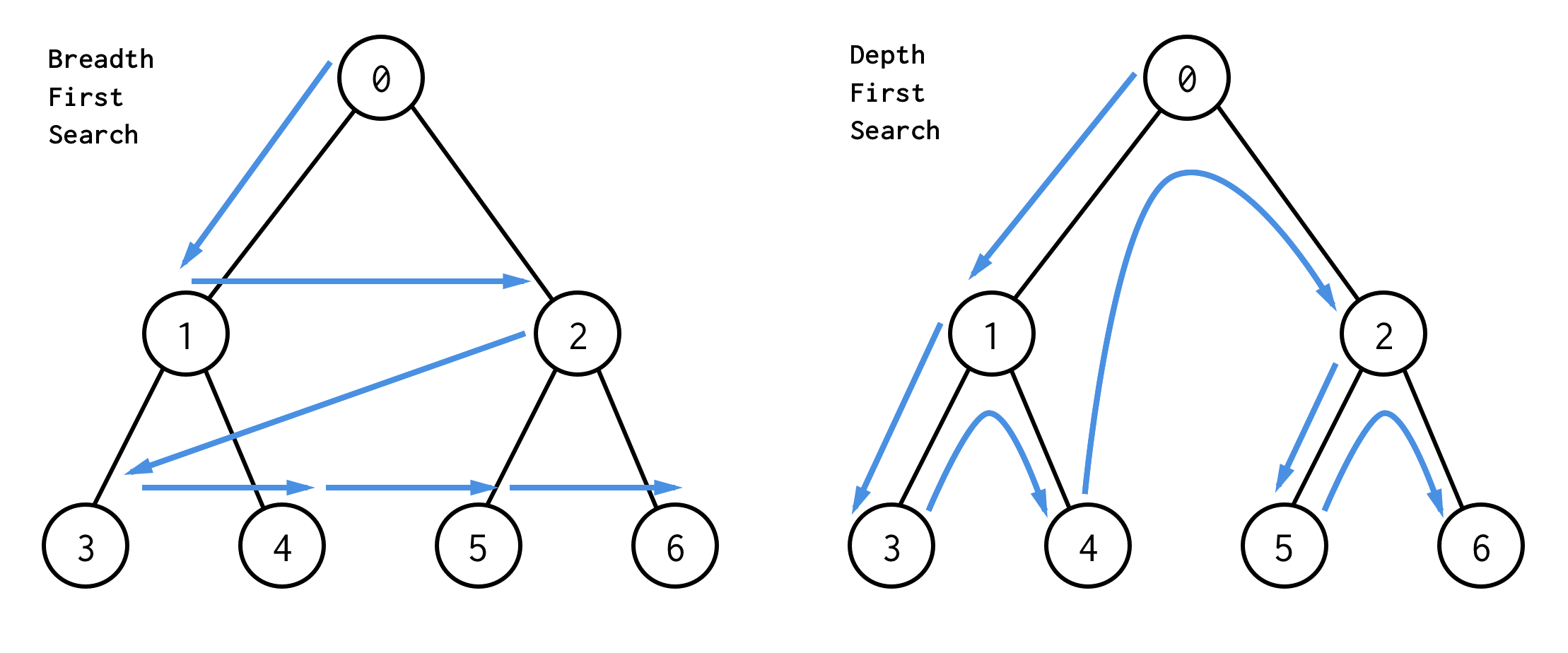
BFS søger i knuder niveau for niveau, startende fra rodknuden. Derefter kontrolleres dens børn. Derefter børn for børn osv. indtil alle knuder er behandlet eller knude, der opfylder søgebetingelsen, er fundet.
DFS opfører sig anderledes. Den kontrollerer alle knuder fra den venstre vej fra roden til bladet, derefter springer den op og kontrollerer højre knude osv.
For klassiske binære træer implementeres BFS ved hjælp af Queue-datastruktur (LinkedList implementerer Queue)
public BinaryNode<T> bfs(Predicate<T> predicate) { Queue<BinaryNode<T>> queue = new LinkedList<>(); queue.offer(this); while (!queue.isEmpty()) { BinaryNode<T> node = queue.poll(); if (predicate.test(node.data)) return node; if (node.left != null) queue.offer(node.left); if (node.right != null) queue.offer(node.right); } return null;}Hvis man erstatter queue med stakken, får man DFS-implementering.
public BinaryNode<T> dfs(Predicate<T> predicate) { Stack<BinaryNode<T>> stack = new Stack<>(); stack.push(this); while (!stack.isEmpty()) { BinaryNode<T> node = stack.pop(); if (predicate.test(node.data)) return node; if (node.right != null) stack.push(node.right); if (node.left != null) stack.push(node.left); } return null;}For eksempel antager vi, at du skal finde en knude med værdien 1 i følgende træ.
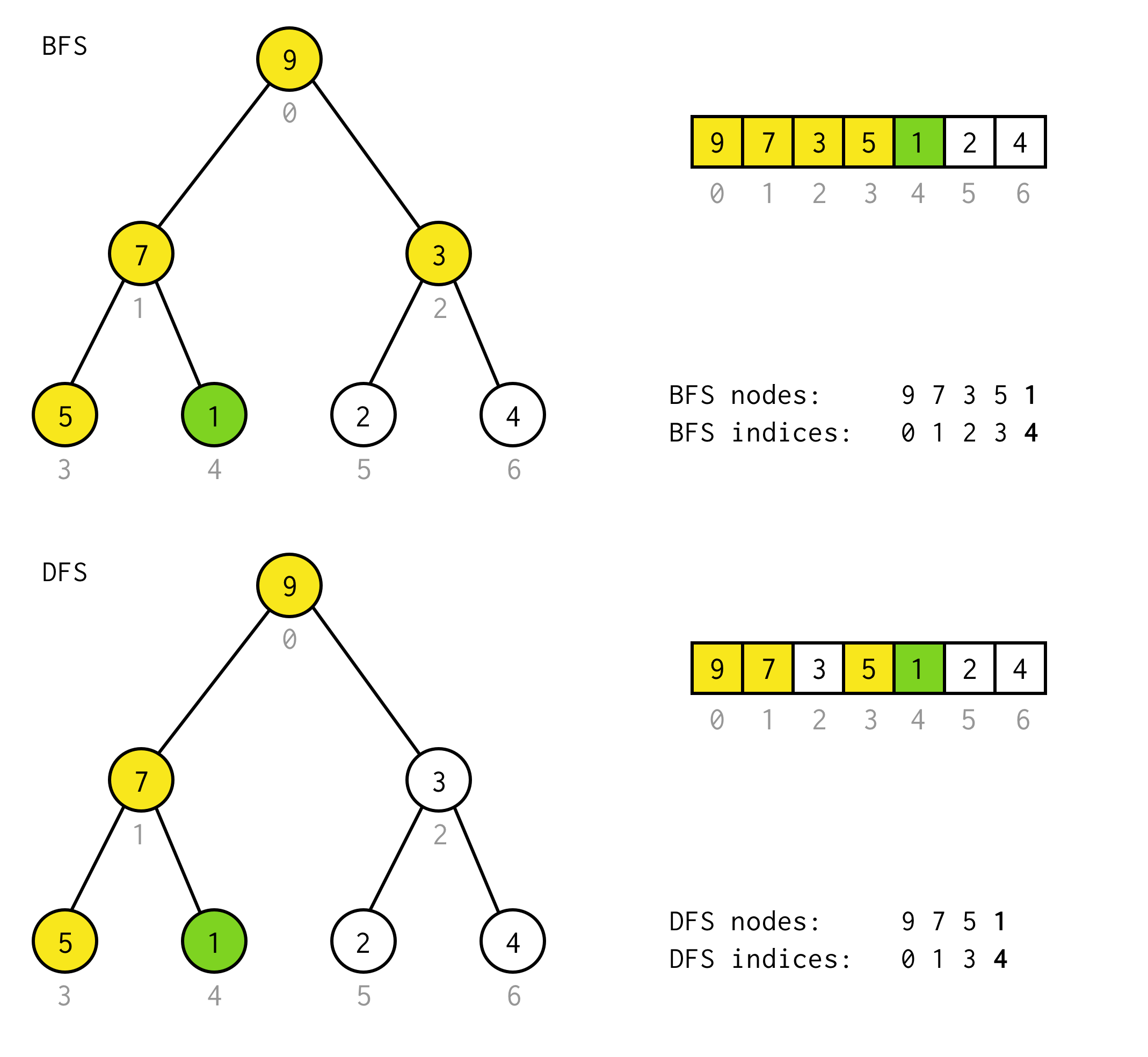
Gule celler er celler, der testes i søgealgoritmen, før den nødvendige knude findes.Tag hensyn til, at DFS i nogle tilfælde kræver færre knuder til behandling.I nogle tilfælde kræver det flere.
BFS og DFS for binære træarray
Breadth-first search for binære træarray er triviel.Da elementerne i binære træarray er placeret niveau for niveau, ogbfs også kontrollerer elementet niveau for niveau, er bfs for binære træarray blot lineær søgning
public int bfs(Predicate<T> predicate) { for (int i = 0; i < array.length; i++) { if (array != null && predicate.test(array)) return i; } return -1; // not found}Depth-first search er lidt vanskeligere.
Ved brug af stakdatastruktur kan det implementeres på samme måde som for klassisk binært træ,bare sæt indekser ind i stakken.
Fra dette punkt er rekursion slet ikke anderledes,du bruger bare implicit metodeopkaldsstakken i stedet for datastrukturstakken.
Hvad nu hvis vi kunne implementere DFS uden stak og rekursion.I sidste ende er det bare et valg af korrekt indeks på hvert trin?
Nå, lad os prøve.
DFS for Binary Tree Array (uden stak og rekursion)
Som i BFS starter vi fra rodindekset 0.
Derpå skal vi inspicere dens venstre barn, hvis indeks kan beregnes ved formel 2*i+1.
Lad os kalde processen med at gå til næste venstre barn fordobling.
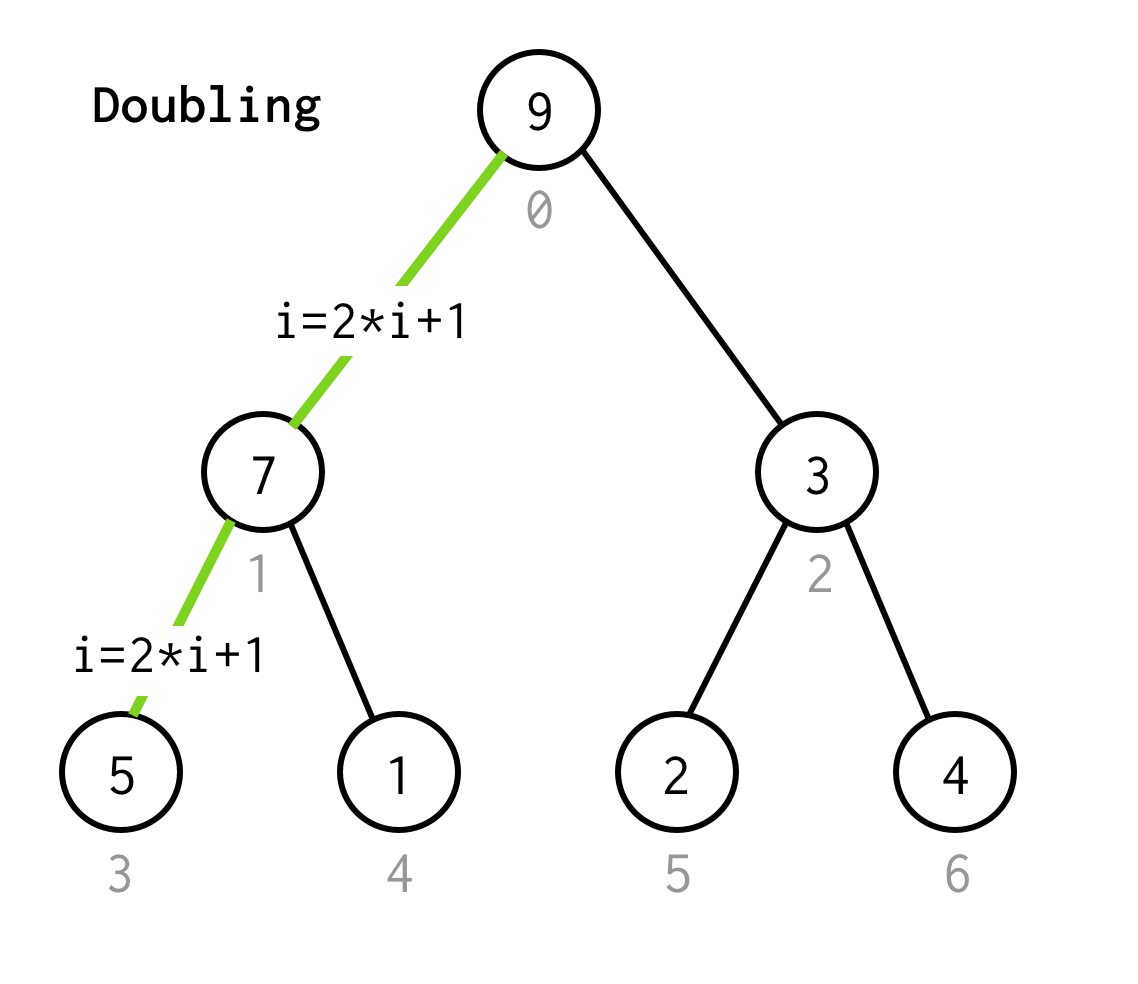
Vi fortsætter med at fordoble indekset, indtil vi ikke stopper ved bladknuden.
Så hvordan kan vi forstå, at det er en bladknude?
Hvis næste venstre barn producerer index out of array bounds exceptionskal vi stoppe fordoblingen og hoppe til det højre barn.
Det er en gyldig løsning, men vi kan undgå unødvendig fordobling.Observationen her er, at antallet af elementer i træet med nogle height er to gange større (og plus en)end træet med height - 1.
For træet med height = 2 har vi 7 elementer, for træet med height = 3 har vi 7*2+1 = 15 elementer.
Med denne observation bygger vi en simpel betingelse
i < array.length / 2Du kan tjekke, at denne betingelse er gyldig for enhver ikke-bladet knude i træet.
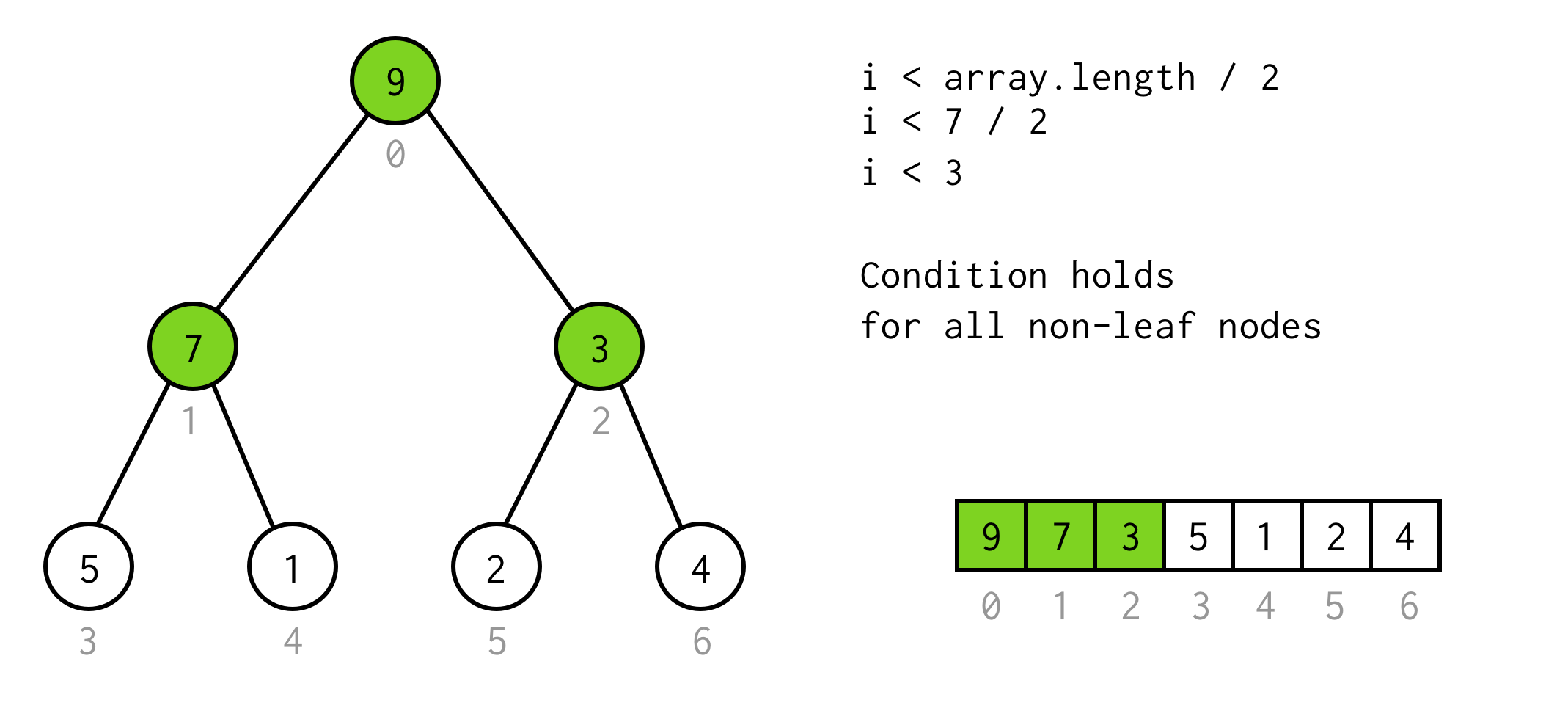
Nice so far. Vi kan køre fordobling, og vi ved endda, hvornår vi skal stoppe. men på denne måde kan vi kun kontrollere venstre børn af knuderne.
Når vi sidder fast ved bladknuden og ikke kan anvende fordobling længere, udfører vi springoperation.Dybest set, hvis fordobling er at gå til venstre barn, er spring at gå til forælder og gå til højre barn.
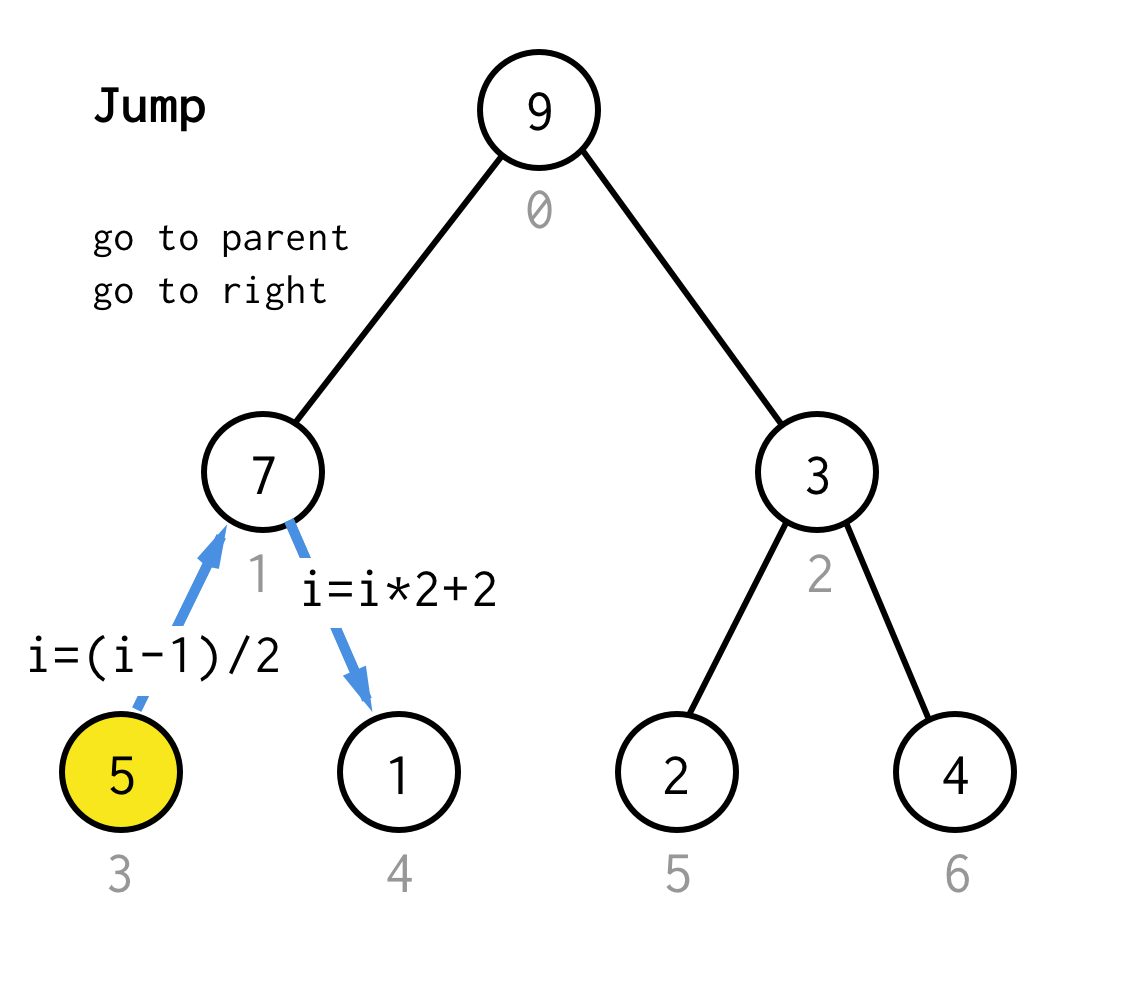
Sådan springoperation kan gennemføres ved blot at øge bladindekset.Men når vi sidder fast i den næste bladknude, flytter en forøgelse ikke knuden til den næste knude, hvilket er nødvendigt for DFS.Så vi er nødt til at lave et dobbelthop
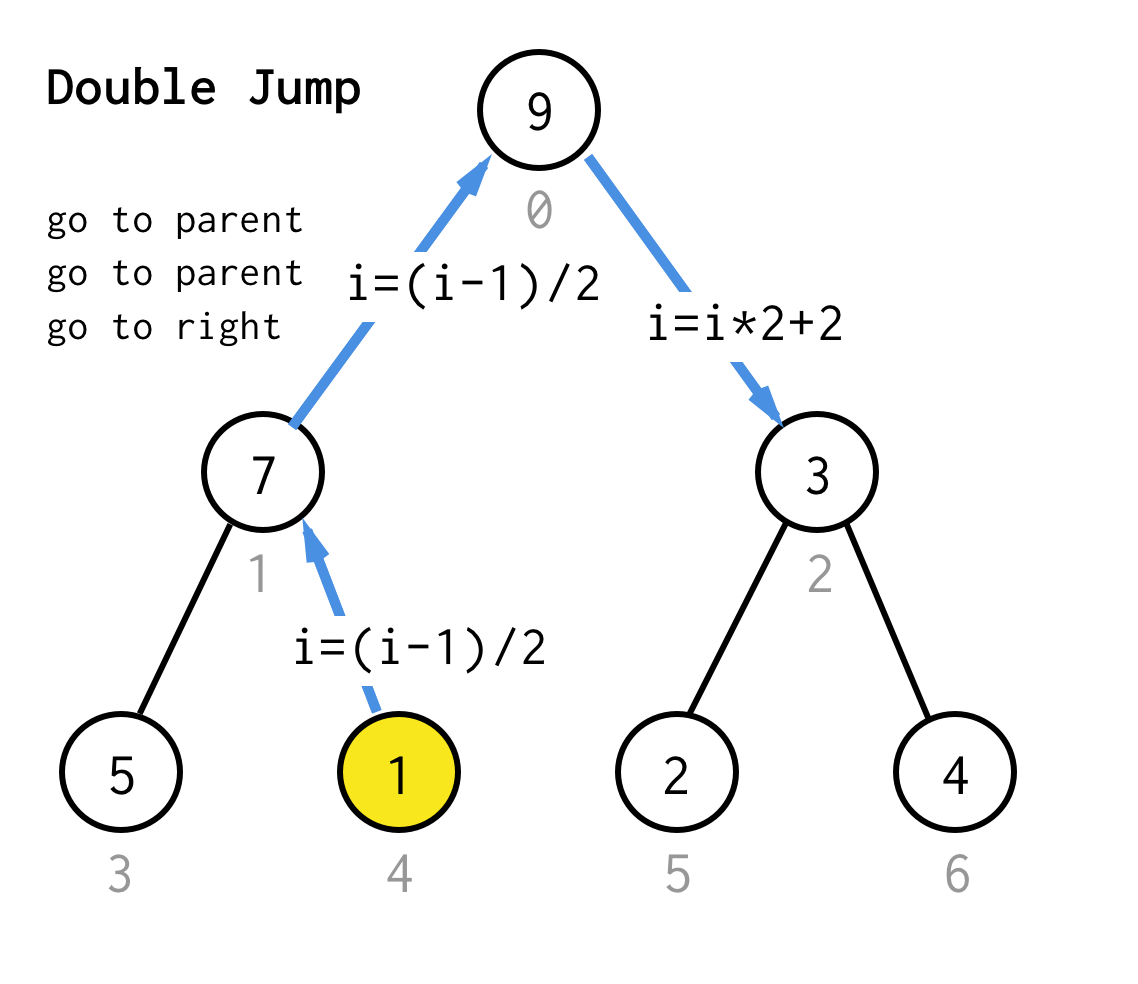
For at gøre det mere generisk kunne vi for vores algoritme definere operationen hop N, som angiver, hvor mange hop til forældrene det kræver, og som altid afsluttes med et hop til det rigtige barn.
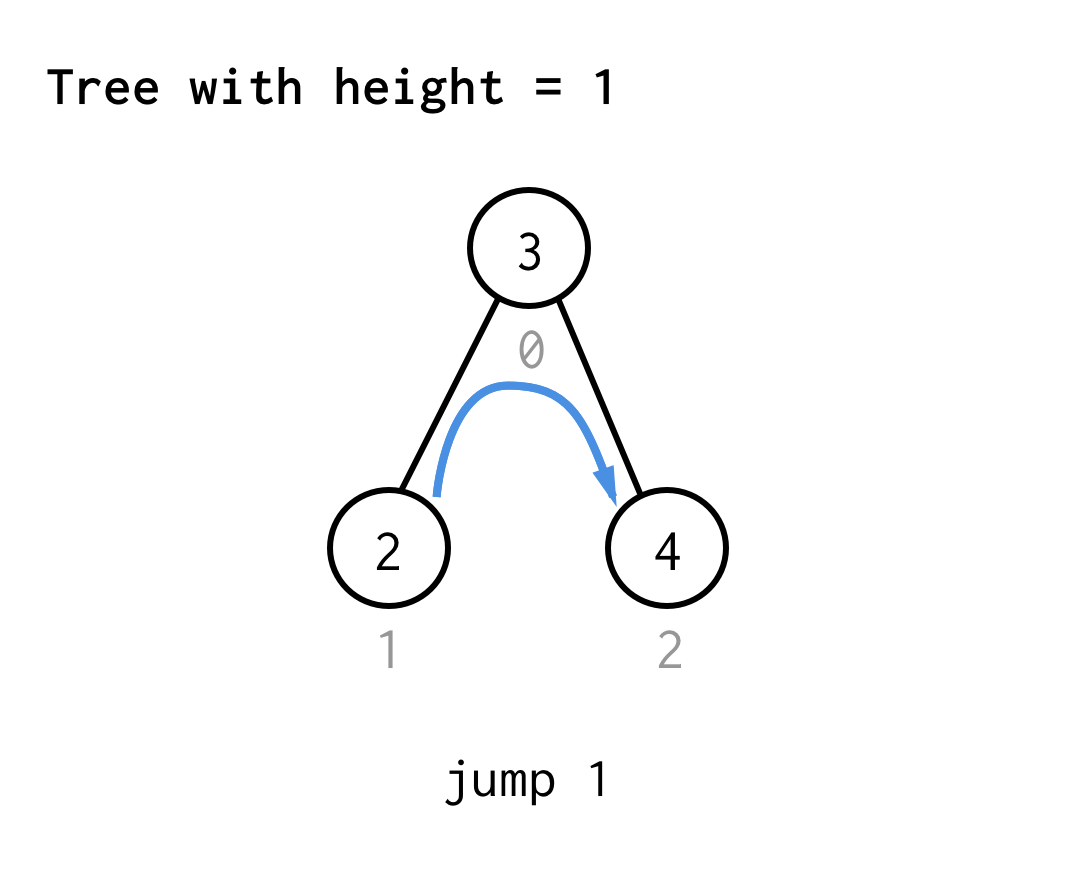
For træet med højde 1 har vi brug for ét hop, hop 1
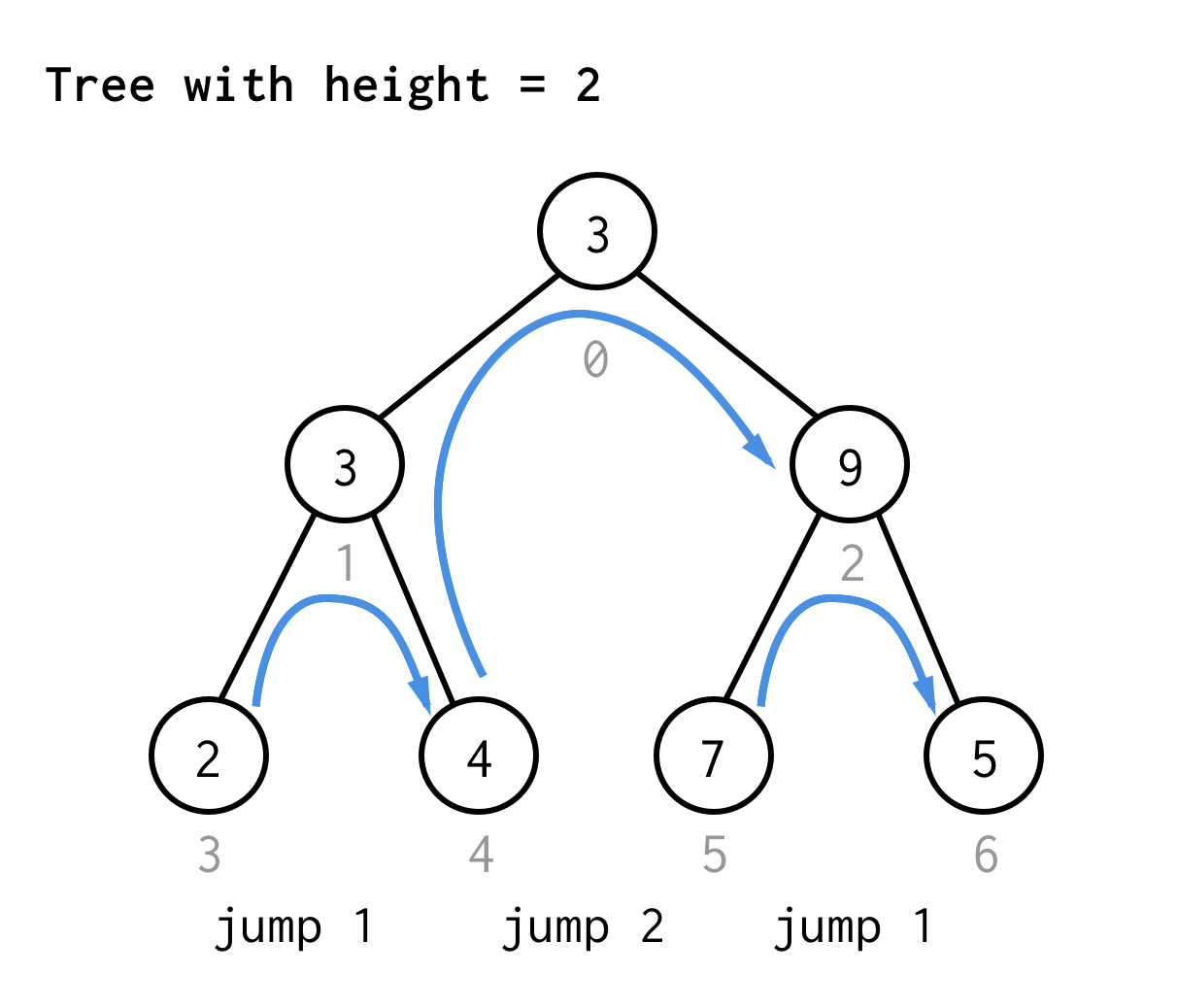
For træet med højde 2 har vi brug for ét hop, ét dobbelthop, og så ét hop igen
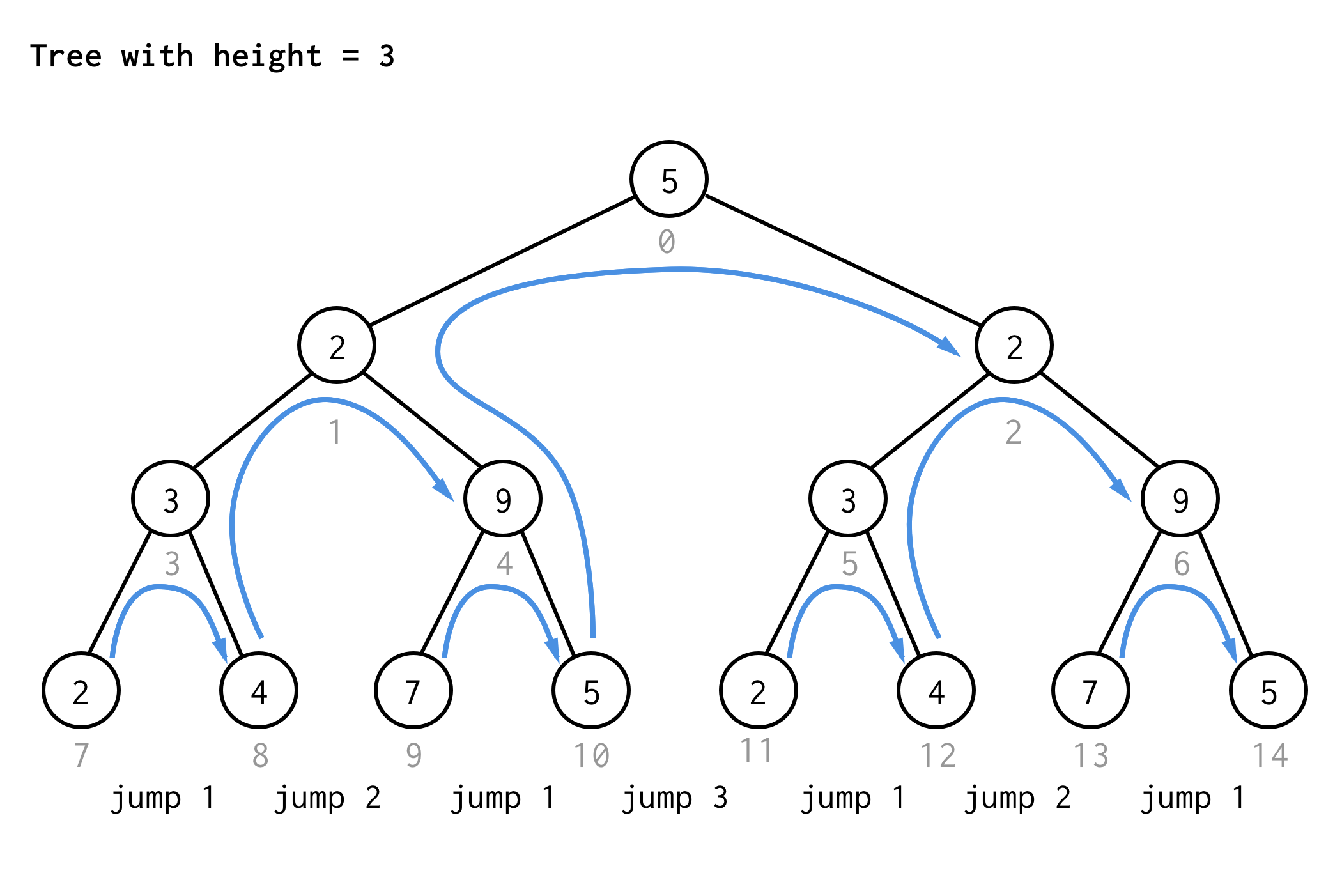
For træet med højde 3 kan man anvende de samme regler og få 7 hop.
Ser du mønsteret?
Hvis du anvender den samme regel på træet med højde 4 og kun skriver springværdierne ned, får du næste sekvensnummer
1 2 1 3 1 2 1 4 1 2 1 3 1 2 1
Denne sekvens er kendt som Zimin-ord, og den har rekursiv definiton,hvilket ikke er godt, fordi vi ikke må bruge rekursion.
Lad os finde en anden måde at beregne det på.
Hvis man ser nøje på springsekvensen, kan man se et ikke-rekursivt mønster.
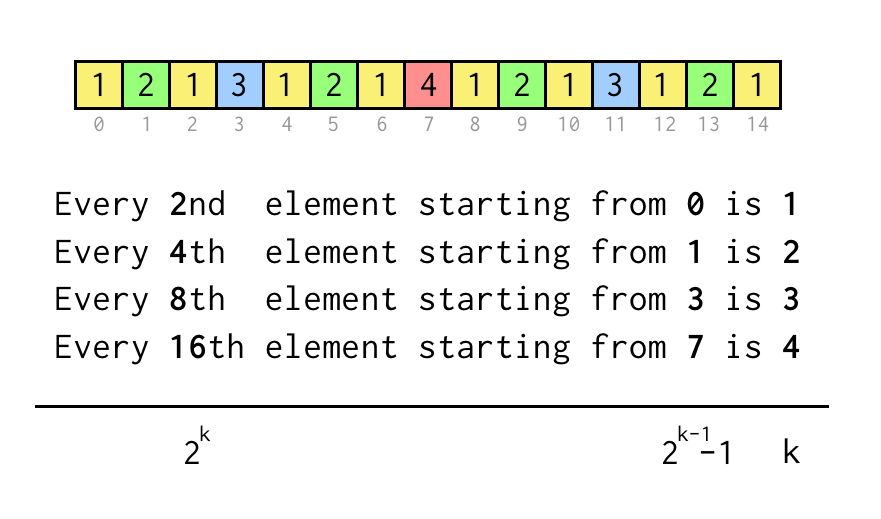
Vi kan spore indeks for det aktuelle blad j, som svarer til indekset i sekvensmatrixen ovenfor.
For at verificere udsagn som “Hvert 8. element starter fra 3” kontrollerer vi blot j % 8 == 3,hvis det er sandt, springer tre spring til den nødvendige overliggende knude.
Iterativ springproces vil være følgende
- Start med
k = 1 - Spring én gang til den overordnede ved at anvende
i = (i - 1)/2 - Hvis
leaf % 2*k == k - 1alle spring er udført, afsluttes - I modsat fald skal
ksættes til2*kog gentages.
Hvis du sætter alt sammen, hvad vi har diskuteret
public int dfs(Predicate<T> predicate) { int i = 0; int leaf = 0; while (i < array.length) { if (array != null && predicate.test(array)) return i; // node found if (i < array.length / 2) { // not leaf node, can be advanced i = 2 * i + 1; // try left child } else { // leaf node, jump int k = 1; while (true) { i = (i - 1) / 2; // jump to the parent int p = k * 2; if (leaf % p == k - 1) break; // correct number of jumps found k = p; } // after we jumped to the parent, go to the right child i = 2 * i + 2; leaf++; // next leaf, please } } return -1;}Fuldført. DFS for binært træ array uden stack og rekursion
Kompleksitet
Kompleksiteten ser ud til at være kvadratisk, fordi vi har loop i en loop,men lad os se, hvad virkeligheden er.
- For halvdelen af de samlede knuder (
n/2) bruger vi fordoblingsstrategi, som er konstantO(1) - For den anden halvdel af de samlede knuder (
n/2) bruger vi bladspringstrategi. - Halvdelen af de bladspringende knuder (
n/4) kræver kun ét forældrespring, 1 iteration.O(1) - Halvdelen af denne halvdel (
n/8) kræver to spring, dvs. 2 iterationer.O(1) - …
- Kun én bladspringende knude kræver fuldt spring til roden, som er
O(logN) - Så, hvis alle tilfælde har
O(1)undtagen ét, som erO(logN), kan vi sige, at gennemsnittet for spring erO(1) - Den samlede kompleksitet er
O(n)
Performance
Selv om teorien er god, så lad os se, hvordan denne algoritme fungerer i praksis, sammenlignet med andre.
Vi tester 5 algoritmer ved hjælp af JMH.
- BFS på binært træ (linked list as queue)
- BFS på binært træ Array (lineær søgning)
- DFS på binært træ (stack)
- DFS on Binary Tree Array (stack)
- Iterativ DFS on Binary Tree Array
Vi har på forhånd oprettet et træ og bruger prædikat til at matche den sidste knude,for at sikre, at vi altid rammer det samme antal knuder for alle algoritmer.
Så, resultater
Benchmark Mode Cnt Score Error Units------------------------------------------------------------------------------------BinaryTreeBenchmarks.bfsOnArray thrpt 200 91378159.672 ± 625885.079 ops/sBinaryTreeBenchmarks.bfsOnBinaryTree thrpt 200 7892439.856 ± 84124.694 ops/sBinaryTreeBenchmarks.dfsOnArray thrpt 200 19980835.346 ± 209143.115 ops/sBinaryTreeBenchmarks.dfsOnBinaryTree thrpt 200 13615106.113 ± 91863.833 ops/sBinaryTreeBenchmarks.dfsOnStackOnArray thrpt 200 11643533.145 ± 87018.132 ops/sObenbart vinder BFS på array. Det er bare en lineær søgning, så hvis du kan repræsentere binært træ som array, så gør det.
Iterativ DFS, som vi lige har beskrevet i artiklen, indtager 2den andenpladsog er 4.5 gange langsommere end lineær søgning (BFS på array)
Resten af de tre algoritmer er endnu langsommere end iterativ DFS, sandsynligvis fordi de involverer yderligere datastrukturer, ekstra plads og hukommelsesallokering.
Og det værste tilfælde er BFS på binært træ. Jeg formoder, at den linkede liste er et problem her.
Slutning
Binary Tree Array er et godt trick til at repræsentere hierarkiske datastrukturer som et statisk array (sammenhængende område i hukommelsen). Det definerer et simpelt indeksforhold til at flytte fra forælder til barn og fra barn til forælder, hvilket ikke er muligt med klassisk binær array-repræsentation. Der findes nogle ulemper, f.eks. langsom indsættelse/sletning, men jeg er sikker på, at der er masser af anvendelser for binære træarrays.
Som vi har vist, er søgealgoritmer, BFS og DFS implementeret på arrays meget hurtigere end deres brødre på en referencebaseret struktur. For virkelige problemer i den virkelige verden er det ikke så vigtigt, og jeg vil sandsynligvis stadig bruge det referencebaserede binære array.
Det var i hvert fald en god øvelse. Forvent spørgsmål “DFS on binary array without recursion and stack” på dit næste interview.
- algoritmer
- datastrukturer
- programmering
mishadoff 10 september 2017
Skriv et svar