Egenvektor

Eigenvektorer er et særligt sæt af vektorer, der er forbundet med et lineært system af ligninger (i.e., en matrixligning), der undertiden også kaldes karakteristiske vektorer, egentlige vektorer eller latente vektorer (Marcus og Minc 1988, s. 144).

Bestemmelsen af et systems egenvektorer og egenværdier er ekstremt vigtig inden for fysik og teknik, hvor den svarer til matrixdiagonalisering og forekommer i så almindelige anvendelser som stabilitetsanalyse, fysik for roterende legemer og små svingninger i vibrerende systemer, for blot at nævne nogle få. Hver egenvektor er parret med en tilsvarende såkaldt egenværdi. Matematisk set skal man skelne mellem to forskellige slags egenvektorer: venstre egenvektorer og højre egenvektorer. For mange problemer inden for fysik og teknik er det imidlertid tilstrækkeligt kun at tage hensyn til højre egenvektorer. Udtrykket “egenvektor”, der anvendes uden forbehold i sådanne anvendelser, kan derfor forstås som en højre egenvektor.

Dekomponering af en kvadratisk matrix i egenværdier og egenvektorer kaldes i dette arbejde for egendekomponering, og det forhold, at denne dekomponering altid er mulig, så længe den matrix, der består af egenvektorerne i , er kvadratisk, er kendt som egendekomponeringssætningen.

Definer en højre egenvektor som en kolonnevektor , der opfylder

(1)

hvor er en matrix, så

(2)

hvilket betyder, at de rigtige egenværdier må have nul determinant, dvs.e.,

(3)

Sådan defineres en venstre egenvektor som en rækkevektor , der opfylder

(4)

Tager man transponeringen af hver side, får man

(5)

som kan omskrives som

(6)

Rediger igen for at få

(7)

hvilket betyder

(8)

Omskrivning giver

		det(A^(T)-det(A^(T)-lambda_LI)	lambda_LI^(T))	(9)
			(10)
			(11)

hvor det sidste trin følger af identiteten

(12)

Geligning af ligningerne (◇) og (11), som begge er lig med 0 for vilkårlige og , kræver derfor, at , dvs, venstre og højre egenværdi er ækvivalente, hvilket ikke er sandt for egenvektorer.

Lad være en matrix dannet af kolonnerne af de højre egenvektorer og være en matrix dannet af rækkerne af de venstre egenvektorer. Lad

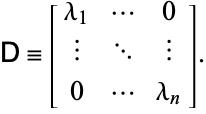(13)

Derpå

				(14)
			(15)

og

			(16)
			(17)

så

(18)

Men denne ligning er af formen

(19)

hvor er en diagonal matrix, så det må være sandt, at også er diagonal. Især hvis er en symmetrisk matrix, så er venstre og højre egenvektor blot hinandens transpositioner, og hvis er en selvadjungeret matrix (dvs. den er hermitisk), så er venstre og højre egenvektor adjungerede matricer.

Eigenvektorer må ikke være lig med nulvektoren. Et skalarisk multiplum af en egenvektor, der ikke er nul, er ækvivalent med den oprindelige egenvektor. Derfor normaliseres egenvektorer ofte, uden tab af almenhed, til enhedslængde.

Mens en matrix altid har egenværdier, hvoraf nogle eller alle kan være degenererede, kan en sådan matrix have mellem 0 og lineært uafhængige egenvektorer. For eksempel har matrixen kun den enkelte egenvektor .

Eigenvektorer kan beregnes i Wolfram Language ved hjælp af Eigenvektorer. Denne kommando returnerer altid en liste af længde , så alle egenvektorer, som ikke er lineært uafhængige, returneres som nulvektorer. Egenvektorer og egenværdier kan returneres sammen ved hjælp af kommandoen Eigensystem.

Givet en matrix med egenvektorer , , og og tilsvarende egenværdier , og , så kan en vilkårlig vektor skrives

(20)

Ved anvendelse af matricen ,

			(21)
			(22)

så

(23)

Hvis , og , følger det derfor, at

(24)

så gentagen anvendelse af matricen på en vilkårlig vektor resulterer på forbløffende vis i en vektor, der er proportional med egenvektoren med den største egenværdi.