Molekylære dipolmomenter
I molekyler, der indeholder mere end én polær binding, er det molekylære dipolmoment blot en vektorkombination af det, der kan betragtes som individuelle “bindingsdipolmomenter”. Matematisk set er dipolmomenter vektorer; de har både en størrelse og en retning. Et molekyls dipolmoment er derfor vektorsummen af dipolmomenterne for de enkelte bindinger i molekylet. Hvis de enkelte bindings dipolmomenter ophæver hinanden, er der ikke noget nettodipolmoment. Det er tilfældet for CO2, et lineært molekyle (figur \(\(\PageIndex{1a}\)). Hver C-O-binding i CO2 er polær, men alligevel viser eksperimenter, at CO2-molekylet ikke har noget dipolmoment. Da de to C-O-bindingsdipoler i CO2 er lige store og orienteret 180° i forhold til hinanden, ophæver de hinanden. Resultatet er, at CO2-molekylet ikke har noget nettodipolmoment, selv om det har en betydelig ladningsadskillelse. H2O-molekylet er derimod ikke lineært (figur \(\PageIndex{1b}\)); det er bøjet i det tredimensionelle rum, så dipolmomenterne ophæver ikke hinanden. Et molekyle som H2O har således et nettodipolmoment. Vi forventer, at koncentrationen af negativ ladning vil være på ilten, det mere elektronegative atom, og positiv ladning på de to hydrogener. Denne ladningspolarisering gør det muligt for H2O at binde hydrogenbindinger til andre polariserede eller ladede arter, herunder andre vandmolekyler.
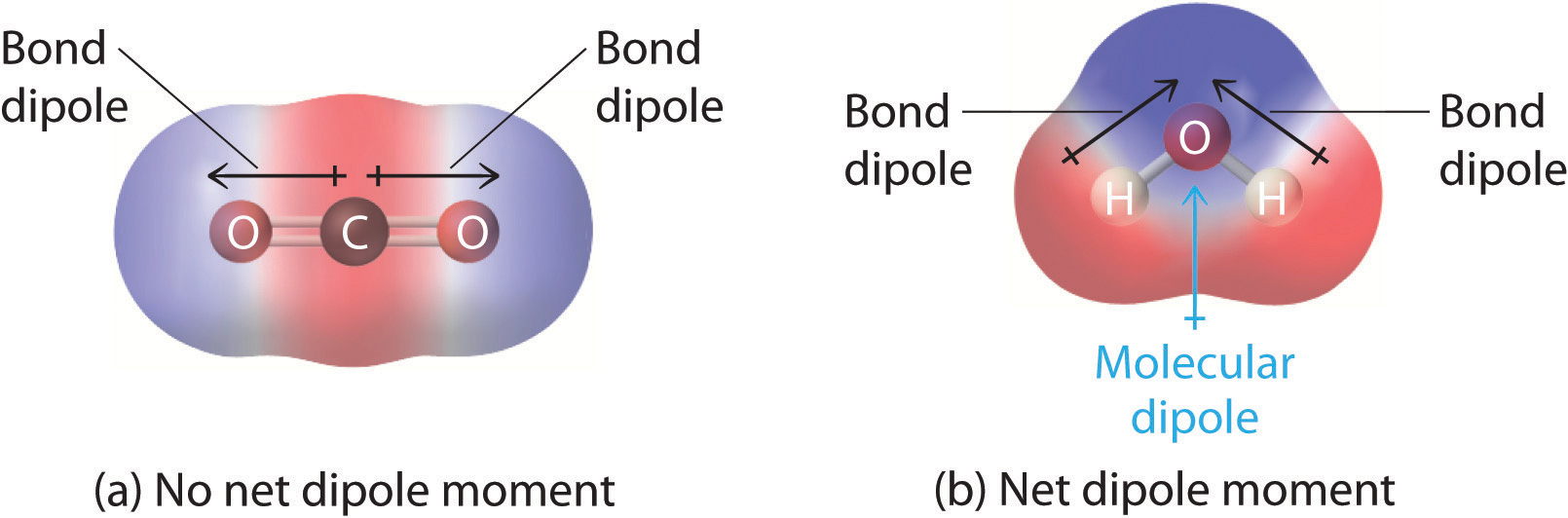
Figur \(\PageIndex{1}\): Hvordan individuelle bindingsdipolmomenter lægges sammen for at give et samlet molekylært dipolmoment for to triatomare molekyler med forskellige strukturer. (a) I CO2 er C-O-båndsdipolerne lige store, men orienteret i modsatte retninger (180°). Deres vektorsum er nul, så CO2 har derfor ingen nettodipol. (b) I H2O er O-H-bindingsdipolerne også lige store, men de er orienteret i 104,5° i forhold til hinanden. Derfor er vektorsummen ikke nul, og H2O har et nettodipolmoment.
Det følgende er en forenklet ligning for et simpelt adskilt to-ladningssystem, som findes i diatomare molekyler eller når man betragter en bindingsdipol inden for et molekyle.
\
Denne bindingsdipol, µ (græsk mu), fortolkes som dipolen fra en ladningsadskillelse over en afstand \(r\) mellem de partielle ladninger \(Q^+\) og \(Q^-\) (eller de mere almindeligt anvendte udtryk \(δ^+\) – \(δ^-\)); dipolens orientering er langs bindingsaksen. Enhederne for dipolmomenter er typisk debyer (D), hvor en deby er lig med 3,336 x 1030 coulombmeter (C – m) i SI-enheder. Betragt et simpelt system med en enkelt elektron og en enkelt proton, der er adskilt af en fast afstand. Enhedsladningen på en elektron er 1,60 X 1019 C og proton & elektronen er 100 pm fra hinanden (ca. længden af en typisk kovalent binding), dipolmomentet beregnes som:
\ &= (1,60 \ gange 10^{-19}\, C)(1,00 \ gange 10^{-10} \,m) \nonumber \\\ &= 1,60 \ gange 10^{-29} \,C \cdot m \label{2} \end{align}\]
\ &= 4.80\; D \label{3} \end{align}\]
\(4,80\; D\) er en vigtig referenceværdi og repræsenterer en ren ladning på +1 og -1, der er adskilt med 100 pm. Hvis ladningsadskillelsen blev forøget, øges dipolmomentet imidlertid (lineært):
- Hvis proton og elektron var adskilt med 120 pm:
\
- Hvis proton og elektron var adskilt med 150 pm:
\
- Hvis proton og elektron var adskilt med 200 pm:
\
Eksempel \(\PageIndex{1}\): Vand
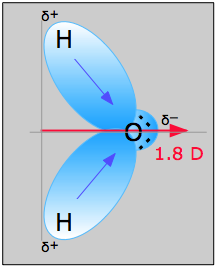
Vandmolekylet i figur \(\(\PageIndex{1}\)) kan bruges til at bestemme dipolmomentets retning og størrelse. Ud fra elektronegativiteterne for oxygen og hydrogen er forskellen 1,2e for hver af hydrogen-oxygenbindingerne. Da ilt er det mere elektronegative atom, udøver det en større tiltrækningskraft på de fælles elektroner; det har også to ensomme elektronpar. Heraf kan det konkluderes, at dipolmomentet peger fra mellem de to hydrogenatomer mod oxygenatomet. Ved hjælp af ovenstående ligning beregnes dipolmomentet til 1,85 D ved at gange afstanden mellem ilt- og brintatomerne med ladningsforskellen mellem dem og derefter finde de komponenter af hver af dem, der peger i retning af nettodipolmomentet (molekylets vinkel er 104.5˚).
Bindingsmomentet for O-H-bindingen =1,5 D, så nettodipolmomentet er
\
Skriv et svar